Autorégressions
Contents
Autorégressions#
Un modèle autorégressif \(\mathrm{AR}(p)\) est exprimé par :
L’outil AutoReg permet d’implémenter des modèles avec :
Termes Déterministes (
trend) :n: Pas de terme déterministe;c: Avec constante (par défaut);ct: Avec constante et tendance temporelle;t: Avec tendance temporelle uniquement;
Variables Indicatrices Saisonnières (i.e. à valeur \(1\) ou \(0\)) (
seasonal) :Truepermet d’inclure \(s-1\) variables indicatrices, où \(s\) est la période de la série.
Termes Déterministes personnalisés (
deterministic) :Prend comme valeur une instance de la classe
DeterministicProcess.
Variables Exogènes (
exog) :Un array ou
dataframede variables exogènes à inclure dans le modèle.
La spécification complète est donc :
où :
\(d_i\) est une variable saisonnière indicatrice, égale à \(1\) si \(t\equiv i\mod s\) où \(s\) est la période de la série. La période \(0\) est exclue si le modèle contient une constante.
\(t\) est une tendance.
\(x_{t,j}\) sont des régresseurs exogènes.
\(\varepsilon_t\) est supposé être un bruit blanc.
%matplotlib inline
import matplotlib.pyplot as plt
import pandas as pd
import pandas_datareader as pdr
import seaborn as sns
from statsmodels.tsa.api import acf, graphics, pacf
from statsmodels.tsa.ar_model import AutoReg, ar_select_order
sns.set_style("darkgrid")
pd.plotting.register_matplotlib_converters()
# Default figure size
sns.mpl.rc("figure", figsize=(20, 12))
sns.mpl.rc("font", size=14)
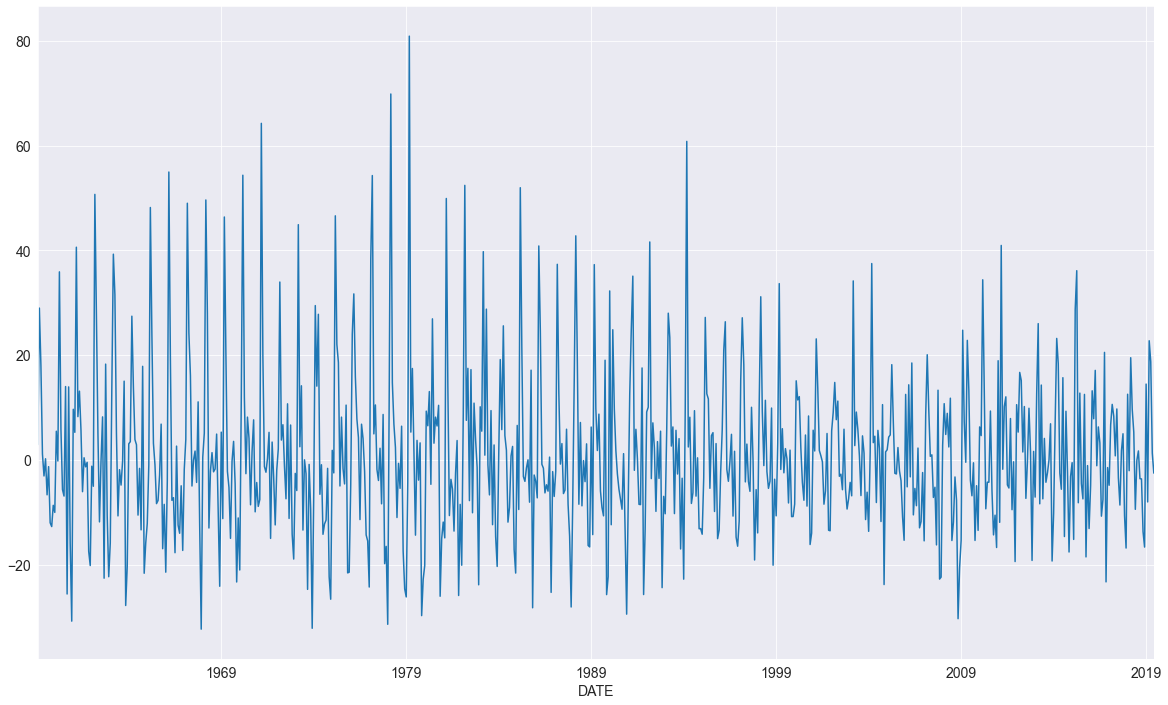
La première série étudiée sera le taux de croissance mensuelle des mises en chantier de logements aux États-Unis, qui n’a pas été corrigé des variations saisonnières. La saisonnalité est évidente compte tenu des pics et des creux réguliers observés.
On met la fréquence de la série temporelle à MS (month-start) pour éviter les erreurs lors de l’utilisation d’AutoReg.
data = pdr.get_data_fred("HOUSTNSA", "1959-01-01", "2019-06-01")
housing = data.HOUSTNSA.pct_change().dropna()
# Multiplication par 100 pour obtenir des pourcentages
housing = 100 * housing.asfreq("MS")
fig, ax = plt.subplots()
ax = housing.plot(ax=ax)
On commence dans un premier temps par ajuster un modèle \(\mathrm{AR}(3)\).
mod = AutoReg(housing, 3, old_names=False)
res = mod.fit()
print(res.summary())
AutoReg Model Results
==============================================================================
Dep. Variable: HOUSTNSA No. Observations: 725
Model: AutoReg(3) Log Likelihood -2993.442
Method: Conditional MLE S.D. of innovations 15.289
Date: Thu, 05 Jan 2023 AIC 5996.884
Time: 23:25:07 BIC 6019.794
Sample: 05-01-1959 HQIC 6005.727
- 06-01-2019
===============================================================================
coef std err z P>|z| [0.025 0.975]
-------------------------------------------------------------------------------
const 1.1228 0.573 1.961 0.050 0.000 2.245
HOUSTNSA.L1 0.1910 0.036 5.235 0.000 0.120 0.263
HOUSTNSA.L2 0.0058 0.037 0.155 0.877 -0.067 0.079
HOUSTNSA.L3 -0.1939 0.036 -5.319 0.000 -0.265 -0.122
Roots
=============================================================================
Real Imaginary Modulus Frequency
-----------------------------------------------------------------------------
AR.1 0.9680 -1.3298j 1.6448 -0.1499
AR.2 0.9680 +1.3298j 1.6448 0.1499
AR.3 -1.9064 -0.0000j 1.9064 -0.5000
-----------------------------------------------------------------------------
La méthode ar_select_order permet de renvoyer les ordres -inférieurs à un ordre passé en paramètre- adéquats pour l’ajustement d’un modèle \(\mathrm{AR}\) à un jeu de données.
sel = ar_select_order(housing, 13, old_names=False)
print("Les ordres possibles sont : ", sel.ar_lags)
Les ordres possibles sont : [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13]
Tous les ordres sont possibles. On ajuste alors un modèle \(\mathrm{AR}(13)\) :
res = sel.model.fit()
print(res.summary())
AutoReg Model Results
==============================================================================
Dep. Variable: HOUSTNSA No. Observations: 725
Model: AutoReg(13) Log Likelihood -2676.157
Method: Conditional MLE S.D. of innovations 10.378
Date: Thu, 05 Jan 2023 AIC 5382.314
Time: 23:25:07 BIC 5450.835
Sample: 03-01-1960 HQIC 5408.781
- 06-01-2019
================================================================================
coef std err z P>|z| [0.025 0.975]
--------------------------------------------------------------------------------
const 1.3615 0.458 2.970 0.003 0.463 2.260
HOUSTNSA.L1 -0.2900 0.036 -8.161 0.000 -0.360 -0.220
HOUSTNSA.L2 -0.0828 0.031 -2.652 0.008 -0.144 -0.022
HOUSTNSA.L3 -0.0654 0.031 -2.106 0.035 -0.126 -0.005
HOUSTNSA.L4 -0.1596 0.031 -5.166 0.000 -0.220 -0.099
HOUSTNSA.L5 -0.0434 0.031 -1.387 0.165 -0.105 0.018
HOUSTNSA.L6 -0.0884 0.031 -2.867 0.004 -0.149 -0.028
HOUSTNSA.L7 -0.0556 0.031 -1.797 0.072 -0.116 0.005
HOUSTNSA.L8 -0.1482 0.031 -4.803 0.000 -0.209 -0.088
HOUSTNSA.L9 -0.0926 0.031 -2.960 0.003 -0.154 -0.031
HOUSTNSA.L10 -0.1133 0.031 -3.665 0.000 -0.174 -0.053
HOUSTNSA.L11 0.1151 0.031 3.699 0.000 0.054 0.176
HOUSTNSA.L12 0.5352 0.031 17.133 0.000 0.474 0.596
HOUSTNSA.L13 0.3178 0.036 8.937 0.000 0.248 0.388
Roots
==============================================================================
Real Imaginary Modulus Frequency
------------------------------------------------------------------------------
AR.1 1.0913 -0.0000j 1.0913 -0.0000
AR.2 0.8743 -0.5018j 1.0080 -0.0829
AR.3 0.8743 +0.5018j 1.0080 0.0829
AR.4 0.5041 -0.8765j 1.0111 -0.1669
AR.5 0.5041 +0.8765j 1.0111 0.1669
AR.6 0.0056 -1.0530j 1.0530 -0.2491
AR.7 0.0056 +1.0530j 1.0530 0.2491
AR.8 -0.5263 -0.9335j 1.0716 -0.3317
AR.9 -0.5263 +0.9335j 1.0716 0.3317
AR.10 -0.9525 -0.5880j 1.1194 -0.4120
AR.11 -0.9525 +0.5880j 1.1194 0.4120
AR.12 -1.2928 -0.2608j 1.3189 -0.4683
AR.13 -1.2928 +0.2608j 1.3189 0.4683
------------------------------------------------------------------------------
La méthode plot_predict permet de visualiser les prévisions. Ici, nous produisons un grand nombre de prévisions qui montrent la saisonnalité capturée par le modèle.
fig = res.plot_predict(720, 840)
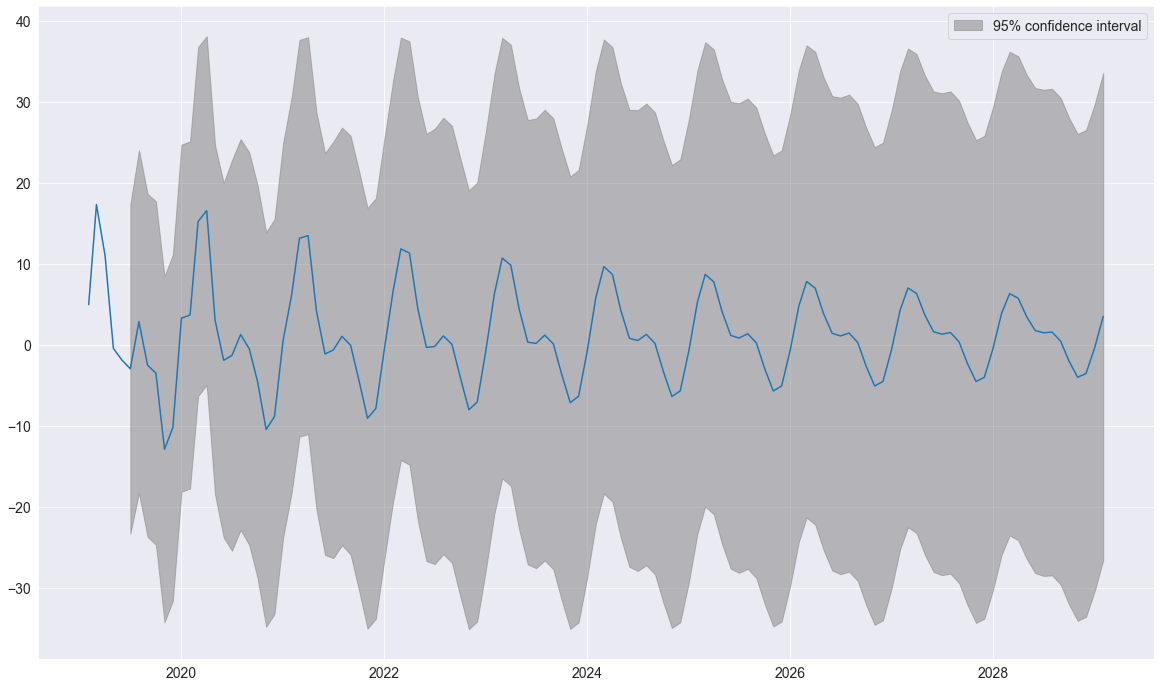
plot_diagnositcs indique si le modèle capture les caractéristiques essentielles des données.
fig = plt.figure(figsize=(16, 9))
fig = res.plot_diagnostics(fig=fig, lags=30)
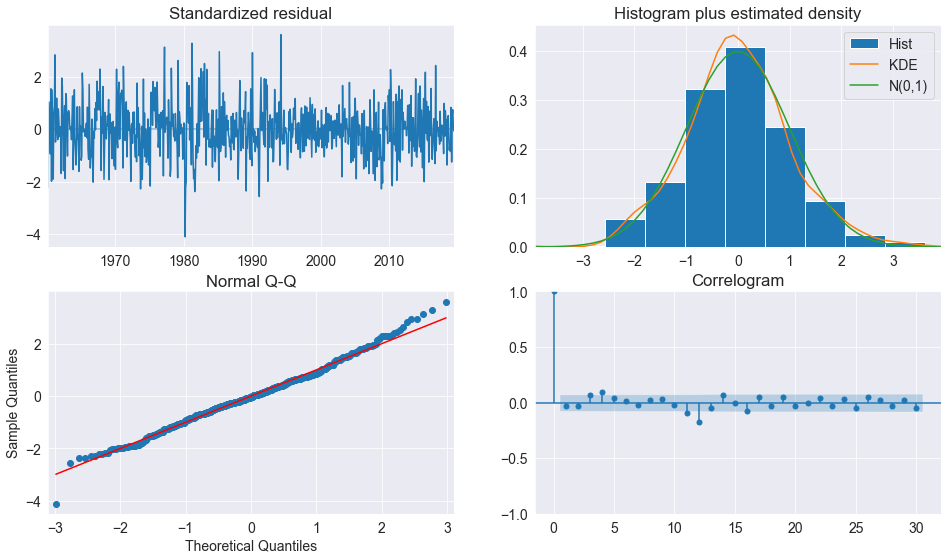
Conclusion
Les résidus standardisés suivent selon toute vraisemblance une distribution gaussienne. Le modèle est donc adapté aux données.
Variables Indicatrices (Dummy)#
AutoReg prend en charge les variables indicatrices saisonnières, lesquelles sont une manière alternative de modéliser la saisonnalité. L’inclusion des dummies raccourcit la modélisation à seulement un \(\mathrm{AR}(2)\).
sel = ar_select_order(housing, 13, seasonal=True, old_names=False)
sel.ar_lags
res = sel.model.fit()
print(res.summary())
AutoReg Model Results
==============================================================================
Dep. Variable: HOUSTNSA No. Observations: 725
Model: Seas. AutoReg(2) Log Likelihood -2652.556
Method: Conditional MLE S.D. of innovations 9.487
Date: Thu, 05 Jan 2023 AIC 5335.112
Time: 23:25:08 BIC 5403.863
Sample: 04-01-1959 HQIC 5361.648
- 06-01-2019
===============================================================================
coef std err z P>|z| [0.025 0.975]
-------------------------------------------------------------------------------
const 1.2726 1.373 0.927 0.354 -1.418 3.963
s(2,12) 32.6477 1.824 17.901 0.000 29.073 36.222
s(3,12) 23.0685 2.435 9.472 0.000 18.295 27.842
s(4,12) 10.7267 2.693 3.983 0.000 5.449 16.005
s(5,12) 1.6792 2.100 0.799 0.424 -2.437 5.796
s(6,12) -4.4229 1.896 -2.333 0.020 -8.138 -0.707
s(7,12) -4.2113 1.824 -2.309 0.021 -7.786 -0.636
s(8,12) -6.4124 1.791 -3.581 0.000 -9.922 -2.902
s(9,12) 0.1095 1.800 0.061 0.952 -3.419 3.638
s(10,12) -16.7511 1.814 -9.234 0.000 -20.307 -13.196
s(11,12) -20.7023 1.862 -11.117 0.000 -24.352 -17.053
s(12,12) -11.9554 1.778 -6.724 0.000 -15.440 -8.470
HOUSTNSA.L1 -0.2953 0.037 -7.994 0.000 -0.368 -0.223
HOUSTNSA.L2 -0.1148 0.037 -3.107 0.002 -0.187 -0.042
Roots
=============================================================================
Real Imaginary Modulus Frequency
-----------------------------------------------------------------------------
AR.1 -1.2862 -2.6564j 2.9514 -0.3218
AR.2 -1.2862 +2.6564j 2.9514 0.3218
-----------------------------------------------------------------------------
Les variables saisonnières sont évidentes dans les prévisions qui ont une composante saisonnière non triviale dans toutes les périodes de 10 ans dans le futur :
fig = res.plot_predict(720, 840)
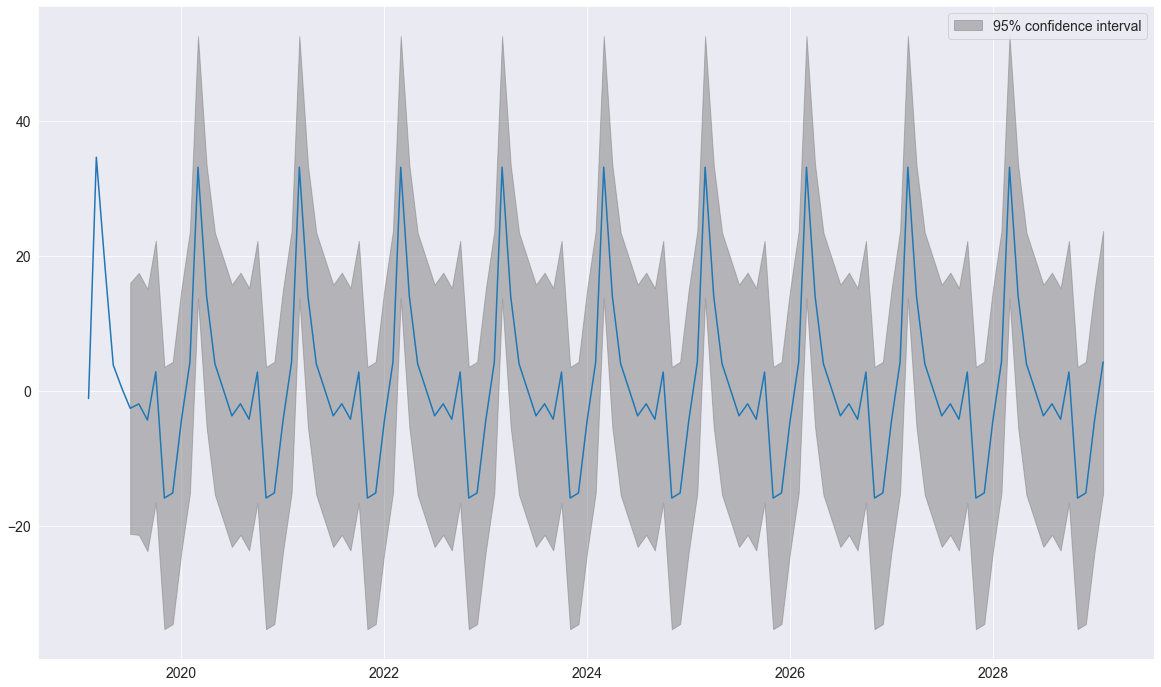
fig = plt.figure(figsize=(16, 9))
fig = res.plot_diagnostics(lags=30, fig=fig)
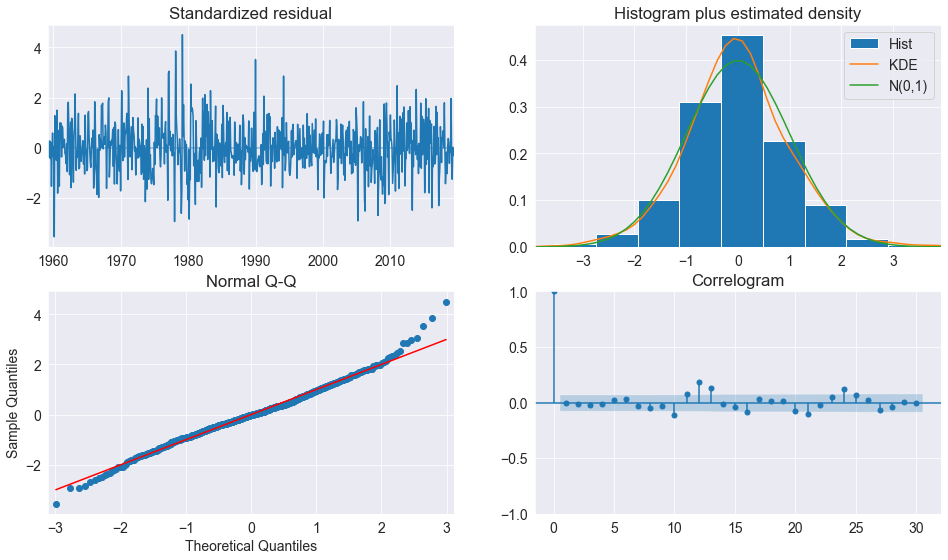
Les résidus standardisés s’apparentent à une réalisation de variables gaussiennes, bien qu’ils comportent des valeurs aberrantes.
Composantes Saisonnières#
Bien qu’AutoReg ne supporte pas directement les composantes saisonnières puisqu’il utilise les moindres carrés ordinaires pour estimer les paramètres, il est possible de capturer la saisonnalité en utilisant un \(\rm AR\) saisonnier avec des paramètres de trop, ce qui n’impose pas de restrictions.
yoy_housing = data.HOUSTNSA.pct_change(12).resample("MS").last().dropna()
_, ax = plt.subplots()
ax = yoy_housing.plot(ax=ax)
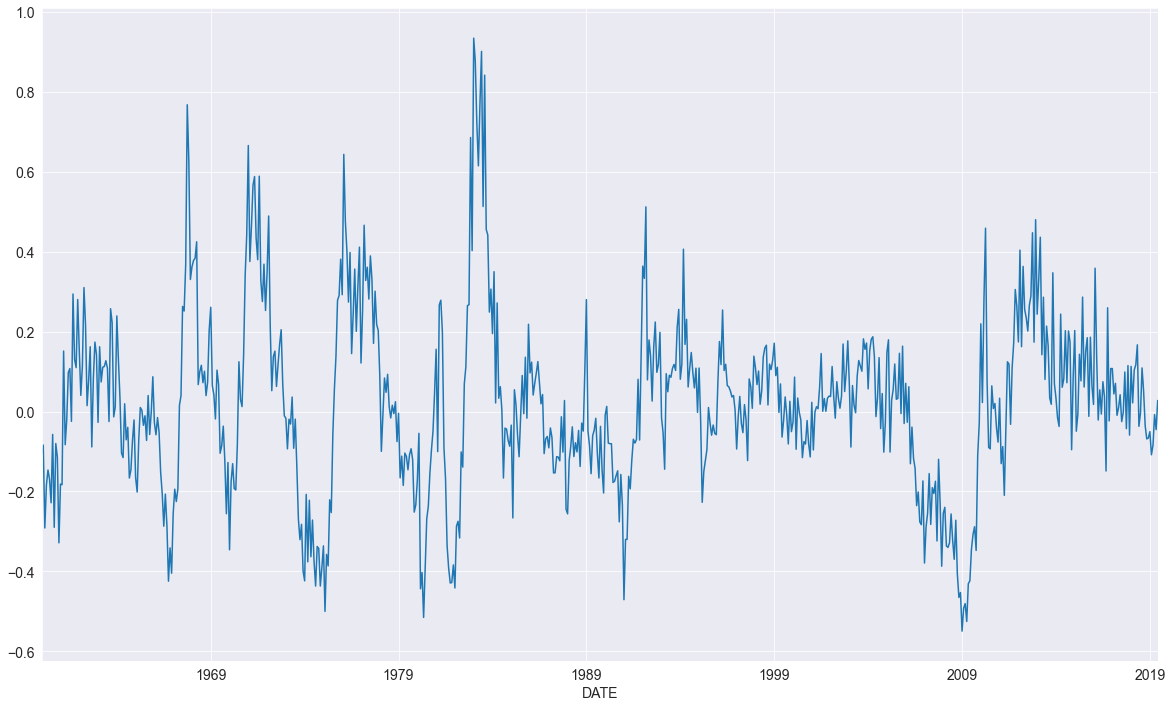
On commence par sélectionner un modèle en utilisant la méthode naïve ne choisissant que le retard maximal. Tous les retards inférieurs sont automatiquement inclus. Le retard maximal à vérifier est fixé à \(13\), car cela permet au modèle de suivre un \(\rm AR\) saisonnier qui comporte à la fois une composante \(\mathrm{AR}(1)\) à court terme et une composante \(\mathrm{AR}(1)\) saisonnière, de sorte que \((1-\phi_s L^{12})(1-\phi_1 L)y_t = \epsilon_t\). Ainsi :
sel = ar_select_order(yoy_housing, 13, old_names=False)
sel.ar_lags
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13]
On constate que tous les ordres sont selectionnés. Nous pouvons mettre glob=True pour rechercher tous les modèles qui incluent jusqu’à 13 retards.
sel = ar_select_order(yoy_housing, 13, glob=True, old_names=False)
sel.ar_lags
[1, 2, 3, 7, 12, 13]
Après avoir ajusté le modèle, nous examinons les graphiques de diagnostic qui indiquent que cette paramétrisation semble être adéquate pour capturer la variation des données.
res = sel.model.fit()
print(res.summary())
AutoReg Model Results
==============================================================================
Dep. Variable: HOUSTNSA No. Observations: 714
Model: Restr. AutoReg(13) Log Likelihood 589.177
Method: Conditional MLE S.D. of innovations 0.104
Date: Thu, 05 Jan 2023 AIC -1162.353
Time: 23:25:19 BIC -1125.933
Sample: 02-01-1961 HQIC -1148.276
- 06-01-2019
================================================================================
coef std err z P>|z| [0.025 0.975]
--------------------------------------------------------------------------------
const 0.0035 0.004 0.875 0.382 -0.004 0.011
HOUSTNSA.L1 0.5640 0.035 16.167 0.000 0.496 0.632
HOUSTNSA.L2 0.2347 0.038 6.238 0.000 0.161 0.308
HOUSTNSA.L3 0.2051 0.037 5.560 0.000 0.133 0.277
HOUSTNSA.L7 -0.0903 0.030 -2.976 0.003 -0.150 -0.031
HOUSTNSA.L12 -0.3791 0.034 -11.075 0.000 -0.446 -0.312
HOUSTNSA.L13 0.3354 0.033 10.254 0.000 0.271 0.400
Roots
==============================================================================
Real Imaginary Modulus Frequency
------------------------------------------------------------------------------
AR.1 -1.0309 -0.2682j 1.0652 -0.4595
AR.2 -1.0309 +0.2682j 1.0652 0.4595
AR.3 -0.7454 -0.7417j 1.0515 -0.3754
AR.4 -0.7454 +0.7417j 1.0515 0.3754
AR.5 -0.3172 -1.0221j 1.0702 -0.2979
AR.6 -0.3172 +1.0221j 1.0702 0.2979
AR.7 0.2419 -1.0573j 1.0846 -0.2142
AR.8 0.2419 +1.0573j 1.0846 0.2142
AR.9 0.7840 -0.8303j 1.1420 -0.1296
AR.10 0.7840 +0.8303j 1.1420 0.1296
AR.11 1.0730 -0.2386j 1.0992 -0.0348
AR.12 1.0730 +0.2386j 1.0992 0.0348
AR.13 1.1193 -0.0000j 1.1193 -0.0000
------------------------------------------------------------------------------
fig = plt.figure(figsize=(16, 9))
fig = res.plot_diagnostics(fig=fig, lags=30)
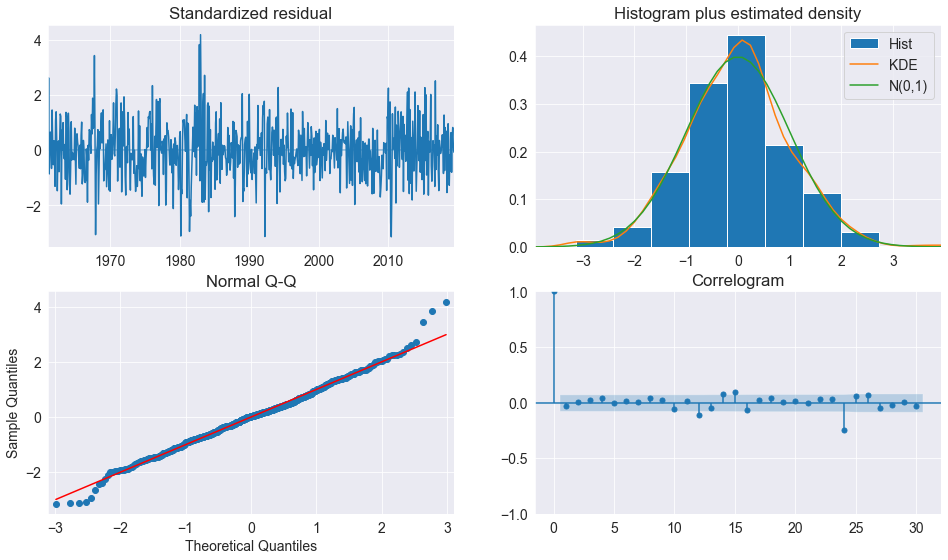
Remarque
Il est possible d’inclure des variables saisonnières indicatrices (dummies), mais cela importera peu dès lors que le modèle a une fréquence annuelle.
Cas d’école : Production Industrielle#
Cette section a trait aux prévisions à la lumière du jeu de données de l’indice de production industrielle de pandas.
data = pdr.get_data_fred("INDPRO", "1959-01-01", "2019-06-01")
ind_prod = data.INDPRO.pct_change(12).dropna().asfreq("MS")
_, ax = plt.subplots(figsize=(20, 12))
ind_prod.plot(ax=ax)
<AxesSubplot:xlabel='DATE'>
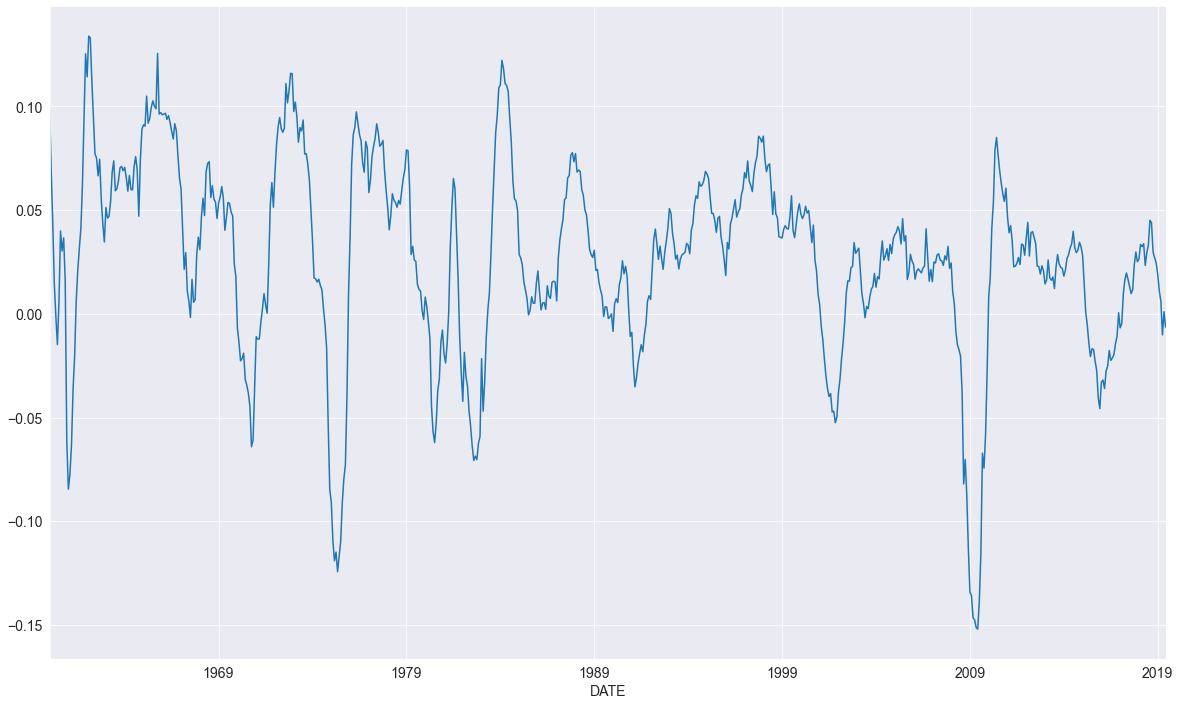
En premier lieu, on sélectionne un modèle utilisant jusqu’à \(12\) retards. Un \(\mathrm{AR}(13)\) minimise le critère \(\rm BIC\) même si de nombreux coefficients sont non significatifs.
sel = ar_select_order(ind_prod, 13, "bic", old_names=False)
res = sel.model.fit()
print(res.summary())
AutoReg Model Results
==============================================================================
Dep. Variable: INDPRO No. Observations: 714
Model: AutoReg(13) Log Likelihood 2322.270
Method: Conditional MLE S.D. of innovations 0.009
Date: Thu, 05 Jan 2023 AIC -4614.540
Time: 23:25:20 BIC -4546.252
Sample: 02-01-1961 HQIC -4588.144
- 06-01-2019
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const 0.0012 0.000 2.779 0.005 0.000 0.002
INDPRO.L1 1.1582 0.035 33.196 0.000 1.090 1.227
INDPRO.L2 -0.0824 0.053 -1.546 0.122 -0.187 0.022
INDPRO.L3 -0.0015 0.053 -0.028 0.977 -0.105 0.102
INDPRO.L4 0.0102 0.053 0.194 0.846 -0.093 0.114
INDPRO.L5 -0.1339 0.053 -2.548 0.011 -0.237 -0.031
INDPRO.L6 -0.0084 0.052 -0.161 0.872 -0.111 0.094
INDPRO.L7 0.0556 0.052 1.065 0.287 -0.047 0.158
INDPRO.L8 -0.0303 0.052 -0.582 0.561 -0.132 0.072
INDPRO.L9 0.0939 0.052 1.807 0.071 -0.008 0.196
INDPRO.L10 -0.0834 0.052 -1.604 0.109 -0.185 0.019
INDPRO.L11 0.0019 0.052 0.037 0.971 -0.100 0.104
INDPRO.L12 -0.3827 0.052 -7.381 0.000 -0.484 -0.281
INDPRO.L13 0.3615 0.033 11.006 0.000 0.297 0.426
Roots
==============================================================================
Real Imaginary Modulus Frequency
------------------------------------------------------------------------------
AR.1 -1.0400 -0.2913j 1.0801 -0.4565
AR.2 -1.0400 +0.2913j 1.0801 0.4565
AR.3 -0.7802 -0.8045j 1.1207 -0.3726
AR.4 -0.7802 +0.8045j 1.1207 0.3726
AR.5 -0.2726 -1.0538j 1.0885 -0.2903
AR.6 -0.2726 +1.0538j 1.0885 0.2903
AR.7 0.2715 -1.0506j 1.0851 -0.2097
AR.8 0.2715 +1.0506j 1.0851 0.2097
AR.9 0.8010 -0.7286j 1.0828 -0.1175
AR.10 0.8010 +0.7286j 1.0828 0.1175
AR.11 1.0218 -0.2219j 1.0456 -0.0340
AR.12 1.0218 +0.2219j 1.0456 0.0340
AR.13 1.0558 -0.0000j 1.0558 -0.0000
------------------------------------------------------------------------------
On peut également utiliser une recherche globale qui permet d’introduire des retards plus longs si nécessaire, sans exiger les retards plus courts.
sel = ar_select_order(ind_prod, 13, "bic", glob=True, old_names=False)
sel.ar_lags
[1, 5, 12, 13]
De nombreux retards ont été abandonnés. Le modèle indique qu’il peut y avoir une certaine saisonnalité dans les données.
res_glob = sel.model.fit()
print(res.summary())
AutoReg Model Results
==============================================================================
Dep. Variable: INDPRO No. Observations: 714
Model: AutoReg(13) Log Likelihood 2322.270
Method: Conditional MLE S.D. of innovations 0.009
Date: Thu, 05 Jan 2023 AIC -4614.540
Time: 23:25:30 BIC -4546.252
Sample: 02-01-1961 HQIC -4588.144
- 06-01-2019
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const 0.0012 0.000 2.779 0.005 0.000 0.002
INDPRO.L1 1.1582 0.035 33.196 0.000 1.090 1.227
INDPRO.L2 -0.0824 0.053 -1.546 0.122 -0.187 0.022
INDPRO.L3 -0.0015 0.053 -0.028 0.977 -0.105 0.102
INDPRO.L4 0.0102 0.053 0.194 0.846 -0.093 0.114
INDPRO.L5 -0.1339 0.053 -2.548 0.011 -0.237 -0.031
INDPRO.L6 -0.0084 0.052 -0.161 0.872 -0.111 0.094
INDPRO.L7 0.0556 0.052 1.065 0.287 -0.047 0.158
INDPRO.L8 -0.0303 0.052 -0.582 0.561 -0.132 0.072
INDPRO.L9 0.0939 0.052 1.807 0.071 -0.008 0.196
INDPRO.L10 -0.0834 0.052 -1.604 0.109 -0.185 0.019
INDPRO.L11 0.0019 0.052 0.037 0.971 -0.100 0.104
INDPRO.L12 -0.3827 0.052 -7.381 0.000 -0.484 -0.281
INDPRO.L13 0.3615 0.033 11.006 0.000 0.297 0.426
Roots
==============================================================================
Real Imaginary Modulus Frequency
------------------------------------------------------------------------------
AR.1 -1.0400 -0.2913j 1.0801 -0.4565
AR.2 -1.0400 +0.2913j 1.0801 0.4565
AR.3 -0.7802 -0.8045j 1.1207 -0.3726
AR.4 -0.7802 +0.8045j 1.1207 0.3726
AR.5 -0.2726 -1.0538j 1.0885 -0.2903
AR.6 -0.2726 +1.0538j 1.0885 0.2903
AR.7 0.2715 -1.0506j 1.0851 -0.2097
AR.8 0.2715 +1.0506j 1.0851 0.2097
AR.9 0.8010 -0.7286j 1.0828 -0.1175
AR.10 0.8010 +0.7286j 1.0828 0.1175
AR.11 1.0218 -0.2219j 1.0456 -0.0340
AR.12 1.0218 +0.2219j 1.0456 0.0340
AR.13 1.0558 -0.0000j 1.0558 -0.0000
------------------------------------------------------------------------------
plot_predict peut être utilisée pour produire des graphiques de prévision avec des intervalles de confiance. Ici, on trace des prévisions commençant à la dernière observation et se poursuivant pendant \(18\) mois.
ind_prod.shape
(714,)
fig = res_glob.plot_predict(start=714, end=732)
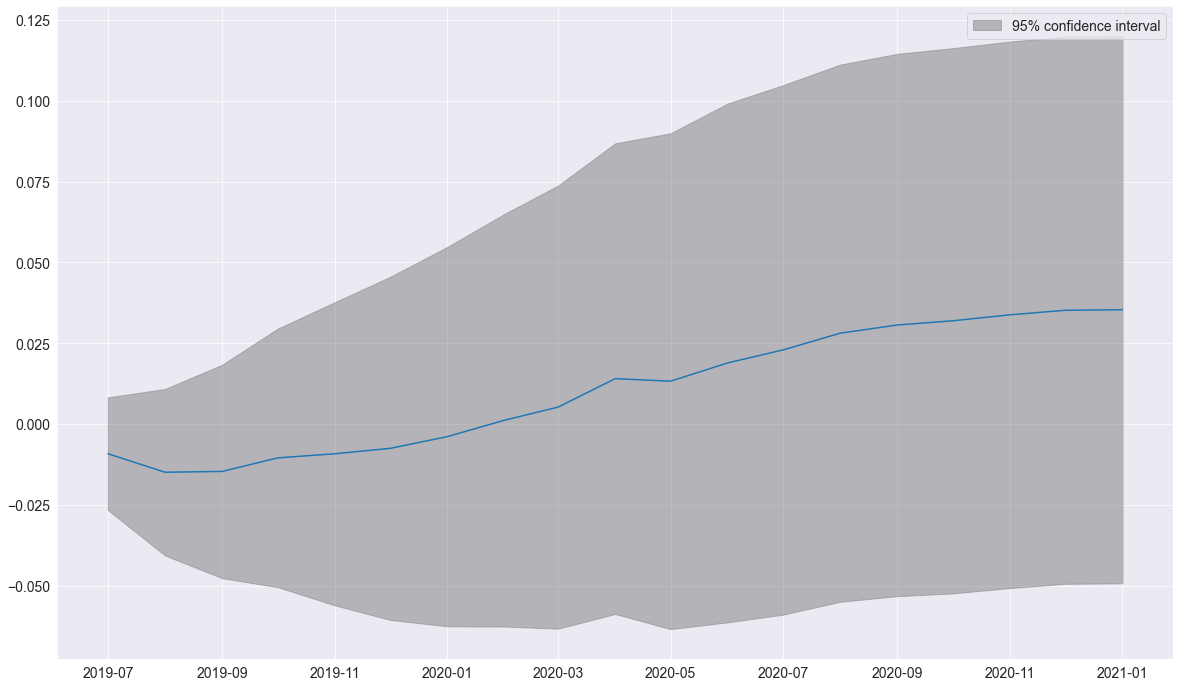
Les prévisions du modèle complet et du modèle restreint sont très similaires. À titre indicatif, on inclut également un \(\mathrm{AR}(5)\) ayant une variation très différente.
res_ar = AutoReg(ind_prod, 5, old_names=False).fit()
predictions = pd.DataFrame({"AR(5)": res_ar.predict(start=714, end=726),"AR(13)": res.predict(start=714, end=726),"AR(13) Restreint": res_glob.predict(start=714, end=726),})
_, ax = plt.subplots()
ax = predictions.plot(ax=ax)
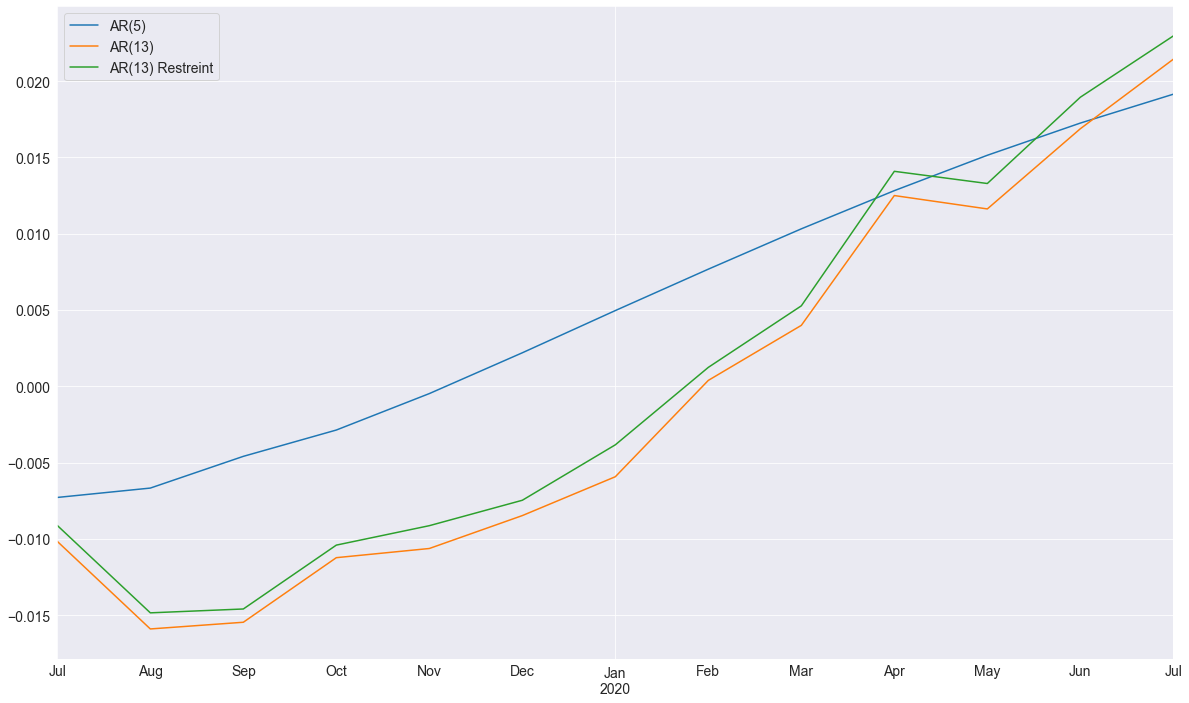
fig = plt.figure(figsize=(20, 12))
fig = res_glob.plot_diagnostics(fig=fig, lags=30)
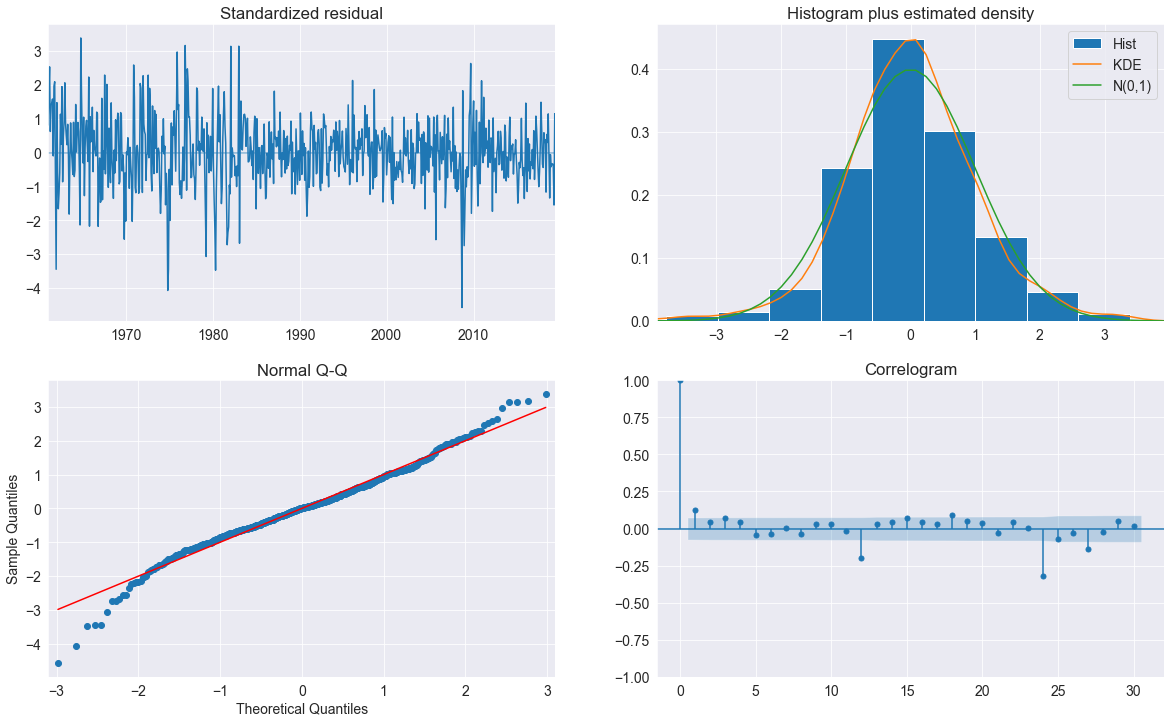
Conclusion
Les diagnostics indiquent que le modèle capture la plupart de la dynamique des données. Le corrélogramme montre une tendance à la fréquence saisonnière et donc un modèle saisonnier plus complet (type \(\rm SARIMAX\)) pourrait être nécessaire.
