Exemple de Régression par les Moindres Carrés (OLS)
Contents
Exemple de Régression par les Moindres Carrés (OLS)#
La méthode canonique du paquet statsmodels pour l’ajustement des modèles de régression linéaire selon le critère des moindres carrés (OLS) est la méthode OLS.
Les paramètres pris en charge par cette fonction :
endog:array-likeUne variable de réponse endogène sous forme d’objet compatible avec les arrays à une dimension
numpy.exog:array-likeUn tableau \(n\times k\) où \(n\) est le nombre d’observations et \(k\) est le nombre de régresseurs. Un terme intercept n’est pas inclus par défaut et doit être spécifié (au moyen de
add_constant).missing:strLes options disponibles sont
none,drop, etraise. Sinone, aucune vérification des valeursnann’est effectuée.dropfait que toutes les observations avec desnansont abandonnées.raisesignale une erreur. La valeur par défaut estnone.
On commence par charger les paquets nécessaires, entre autres matplotlib.pyplot pour le traçage, numpy pour la manipulation des matrices et vecteurs et la génération aléatoire, ainsi que pandas pour le stockage des données.
# Affichage avec la bibliothèque graphique intégrée à Notebook
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import statsmodels.api as sm
from statsmodels.sandbox.regression.predstd import wls_prediction_std
np.random.seed(7890)
Estimation Linéaire par les Moindres Carrés#
On commence par générer un échantillon de \(n=100\) observations du modèle \(y_i=1+0.1x_i+10x_i^2+\varepsilon_i\) où \(\varepsilon_i\sim\mathcal N(0,1)\). Cet échantillon servera de référence pour l’ajustement ci-après du modèle de régression linéaire de la variable \(y\) sur les variables \(x\) et \(x^2\).
n = 100
x = np.linspace(0, 10, 100)
X = np.column_stack((x, x ** 2))
beta = np.array([1, 0.1, 10])
e = np.random.normal(size=n)
Aucune constante n’est ajoutée au modèle. Il faut entasser une colonne de \(1\) manuellement.
X = sm.add_constant(X)
y = np.dot(X, beta) + e
Il s’agit maintenant d’ajuster le modèle de régression linéaire par moindres carrés sur le jeu de donnéees en enchaînant la méthode fit() sur le modèle résultant de l’appel OLS(). Puis, on affiche le résultat par la méthode summary().
res = sm.OLS(y, X).fit()
res.summary()
| Dep. Variable: | y | R-squared: | 1.000 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared: | 1.000 |
| Method: | Least Squares | F-statistic: | 4.053e+06 |
| Date: | Thu, 05 Jan 2023 | Prob (F-statistic): | 1.92e-239 |
| Time: | 23:24:04 | Log-Likelihood: | -146.14 |
| No. Observations: | 100 | AIC: | 298.3 |
| Df Residuals: | 97 | BIC: | 306.1 |
| Df Model: | 2 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| const | 0.6806 | 0.312 | 2.185 | 0.031 | 0.062 | 1.299 |
| x1 | 0.2175 | 0.144 | 1.510 | 0.134 | -0.068 | 0.503 |
| x2 | 9.9890 | 0.014 | 716.877 | 0.000 | 9.961 | 10.017 |
| Omnibus: | 4.487 | Durbin-Watson: | 2.092 |
|---|---|---|---|
| Prob(Omnibus): | 0.106 | Jarque-Bera (JB): | 4.075 |
| Skew: | 0.335 | Prob(JB): | 0.130 |
| Kurtosis: | 3.728 | Cond. No. | 144. |
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Les quantités d’intérêt peuvent être extraites directement du modèle ajusté. dir(results) pour obtenir une liste complète. Voici quelques exemples :
print("Estimations des Paramètres : ", res.params)
print("Coefficient de détermination R2 : ", res.rsquared)
Estimations des Paramètres : [0.6806226 0.21750693 9.98895028]
Coefficient de détermination R2 : 0.9999880324891753
Force est de constater que le coefficient de détermination est proche de 1. Cela traduit que la proportion de la variabilité observée de \(y\) expliquée par le modèle de régression linéaire \(\beta_0+\beta_1x+\beta_2x\) est plus de \(99\%\), confirmant ainsi le modèle théorique de base employé pour générer l’échantillon.
L’estimation des paramètres selon le critère des moindres carrés étant très précise, les paramètres retrouvés avoisinent les valeurs théoriques \(\beta_0=1\), \(\beta_1=0.1\) et \(\beta_2=10\).
Estimation Linéaire en les paramètres par les Moindres Carrés#
Rappel
La désignation linéaire renvoie à la relation entre les paramètres \(\boldsymbol\beta\) et la réponse \(y\). \(y\) est une fonction linéaire par rapport à \(\boldsymbol\beta\), mais pas forcément de(s) variable(s) indépendante(s) (e.g. le modèle \(y=e^x\beta+\varepsilon\) est bel et bien linéaire).
On simule pour cette section un jeu de données artificel avec une relation non-linéaire entre \(x\) et \(y\) : \(y_i=5+0.5x_i+0.5\sin(x_i)-0.02(x_i-5)^2+\varepsilon_i\) avec des erreurs \(\varepsilon_i\sim\mathcal N(0,0.5^2)\). C’est bien un modèle linéaire, car il l’est pour les paramètres.
sig = 0.5
x = np.linspace(0, 20, n)
X = np.column_stack((x, np.sin(x), (x-5)**2, np.ones(n)))
beta = np.array([0.5, 0.5, -0.02, 5.])
y_true = np.dot(X, beta)
y = y_true + sig * np.random.normal(size=n)
res2 = sm.OLS(y, X).fit()
res2.summary()
| Dep. Variable: | y | R-squared: | 0.926 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared: | 0.923 |
| Method: | Least Squares | F-statistic: | 398.0 |
| Date: | Thu, 05 Jan 2023 | Prob (F-statistic): | 5.23e-54 |
| Time: | 23:24:04 | Log-Likelihood: | -73.136 |
| No. Observations: | 100 | AIC: | 154.3 |
| Df Residuals: | 96 | BIC: | 164.7 |
| Df Model: | 3 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| x1 | 0.4919 | 0.019 | 25.340 | 0.000 | 0.453 | 0.530 |
| x2 | 0.3458 | 0.075 | 4.610 | 0.000 | 0.197 | 0.495 |
| x3 | -0.0201 | 0.002 | -11.786 | 0.000 | -0.023 | -0.017 |
| const | 5.1014 | 0.126 | 40.531 | 0.000 | 4.852 | 5.351 |
| Omnibus: | 0.727 | Durbin-Watson: | 2.516 |
|---|---|---|---|
| Prob(Omnibus): | 0.695 | Jarque-Bera (JB): | 0.402 |
| Skew: | 0.141 | Prob(JB): | 0.818 |
| Kurtosis: | 3.131 | Cond. No. | 223. |
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
On peut extraire des quantités d’intérêt par la même façon :
print("Estimation des Paramètres : ", res2.params)
print("Erreurs Standards :", res2.bse)
print("Valeurs Prédites : ", res2.predict())
print("Coefficient de Détermination : ", res2.rsquared)
Estimation des Paramètres : [ 0.4918749 0.34579746 -0.02010405 5.10135543]
Erreurs Standards : [0.01941121 0.07501281 0.0017057 0.1258622 ]
Valeurs Prédites : [ 4.5987543 4.80730058 5.01138378 5.20829662 5.39555668 5.57100744
5.73290593 5.87999367 6.01154786 6.12741073 6.227996 6.31427204
6.38772248 6.45028587 6.50427684 6.55229193 6.597104 6.64154944
6.68841284 6.74031364 6.79959971 6.86825173 6.94780274 7.03927571
7.14314196 7.25930198 7.38708951 7.52529857 7.6722326 7.8257734
7.9834673 8.14262497 8.3004308 8.45405742 8.60078069 8.73809052
8.86379296 8.9760994 9.07369939 9.15581386 9.22222686 9.27329435
9.30992968 9.33356646 9.34610027 9.34981152 9.34727275 9.34124394
9.33456029 9.33001689 9.33025503 9.33765478 9.35423816 9.38158694
9.42077827 9.47234085 9.5362335 9.61184676 9.69802769 9.79312683
9.8950652 10.0014189 10.10951773 10.21655373 10.31969545 10.41620307
10.50353988 10.57947541 10.64217619 10.69028032 10.72295283 10.73991967
10.74147887 10.72848838 10.7023312 10.66485912 10.61831739 10.56525344
10.50841322 10.45062952 10.39470678 10.34330698 10.29884142 10.2633726
10.23853034 10.22544551 10.22470401 10.23632295 10.25974996 10.29388563
10.33712826 10.38743901 10.44242477 10.49943558 10.55567233 10.60830068
10.6545663 10.6919069 10.71805647 10.73113744]
Coefficient de Détermination : 0.9255894581356353
Plus de \(92\%\) de variabilité observée de \(y\) est recensée par le modèle, ce dernier s’adapte significativement bien aux données. Les estimations des paramètres sont au voisinage des paramètres théoriques réels : \(\beta_1=0.5\), \(\beta_2=0.5\), \(\beta_3=-0.02\) et \(\beta_0=5\).
Il est possible de tracer un graphique pour comparer les valeurs sans bruit (i.e. sans \(\varepsilon\)) du modèle aux prédictions par les moindres carrés ordinaires. Les intervalles de prédictions sont construits à l’aide de la commande wls_prediction_std.
pfstd, iv_sup, iv_inf = wls_prediction_std(res2)
fig, ax = plt.subplots(figsize=(15,6))
ax.plot(x, y, 'o', label = 'Valeurs Réelles')
ax.plot(x, y_true, 'b-', label='Valeurs Sans Bruit')
ax.plot(x, res2.fittedvalues, 'r--', label='Valeurs Ajustées')
ax.plot(x, iv_sup, 'g--', label="Intervalle de Prédiction")
ax.plot(x, iv_inf, 'g--')
ax.legend(loc="best")
<matplotlib.legend.Legend at 0x14b9166b0>
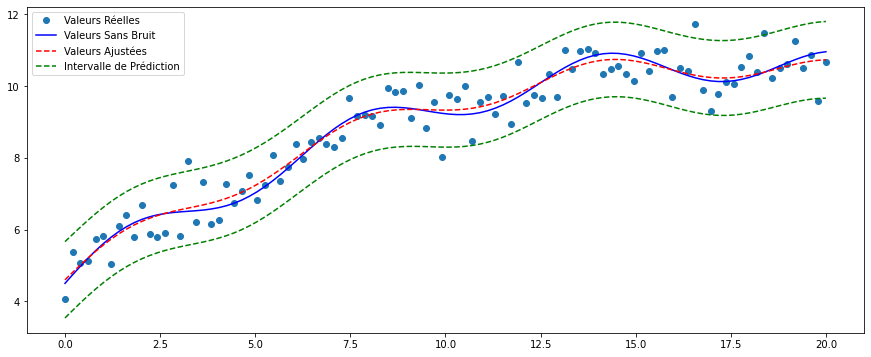
Les valeurs ajustées sont à peu près identiques aux valeurs sans bruit, ce qui confirme la significativité de l’ajustement du modèle susmentionné aux données. L’intervalle de prédiction encapsule aussi l’écrasante majorité des valeurs observée, de par sa définition.
