Ajustement d’un Modèle Linéaire Généralisé
Contents
Ajustement d’un Modèle Linéaire Généralisé#
La méthode idoine pour ajuster des modèles linéaires généralisés au sein du paquet statsmodels est GLM. Les paramètres à spécifier sont :
endog:array-likeUne variable de réponse endogène sous forme de tableau à une ou deux dimensions à l’image des arrays
numpy. Les modèles de la famille binomiale prennent en charge un tableau à deux colonnes, où chaque observation est supposée être sous format[succès, échec].exog:array-likeUn tableau \(n\times k\) où \(n\) est le nombre d’observations et \(k\) est le nombre de régresseurs. Un terme intercept n’est pas inclus par défaut et doit être spécifié (au moyen de
add_constant). Les modèles définis au travers des formules comprennent une constante par construction.family: Instance de la classestatsmodels.api.familyPar défaut, correspond à la distribution gaussienne. Chaque constructeur de famille peut prendre en argument une fonction de lien (i.e. objet de type
statsmodels.api.families.family.<familyname>.Link). Les familles de distributions implémentées sont :Family(link, variance): Classe parente pour les familles exponentielles;Binomial([link]): Distribution binomiale de la famille exponentielle;Gamma([link]): Distribution Gamma de la famille exponentielle;Gaussian([link]): Loi normale gaussienne;InverseGaussian([link]): Loi normale inverse;NegativeBinomial([link, alpha]): Loi binomiale négative;Poisson([link]): Loi de Poisson de la famille exponentielle.
Les fonctions de liens prises en charge par une distribution peuvent être obtenues via
sm.families.family.<familyname>.links. Les fonctions les plus courantes sont :Log(),Logit(),probit(),identity()…Seules ces combinaisons sont licites pour les familles et les fonctions de lien :
Family
identloglogitprobitcloglogpowopownbinomlogloglogcGaussienne
x
x
x
x
x
x
x
x
x
Inv-Gaussienne
x
x
x
Binomiale
x
x
x
x
x
x
x
x
x
Poisson
x
x
x
Binomiale Négative
x
x
x
x
Gamma
x
x
x
Tweedie
x
x
x
offset:array_likeouNoneUn décalage ou offset à ajouter au modèle. Auquel cas, doit être un array dont la longueur est égale au nombre de lignes
exog.exposure:array_likeouNoneUne variable d’exposition ou exposure, qui indique combien de temps a duré l’exposition ou le nombre de fois où l’événement pourrait avoir eu lieu. Le cas échéant,
Log(exposure)sera ajouté à la prédiction linéaire du modèle. Doit correspondre à un array de même longueur queendog.
Attention
La variable d’exposition n’est valide uniquement lorsque la fonction de lien est logarithmique!
freq_weights:array_likeUn tableau à une dimension définissant les poids des fréquences des observations. À défaut de valeur, l’algorithme remplace cet argument par un array constitué de \(1\) et de longueur identique à celle de la variable
endog. Les poids des fréquences produisent les mêmes résultats que la répétition des observations au nombre des fréquences. Les pondérations de fréquence maintiennent le nombre d’observations cohérent, mais les degrés de liberté changent pour refléter les nouveaux poids.var_weights:array_likeUn tableau à une dimension déterminant les poids des variances. À défaut de valeur, l’algorithme remplace cet argument par un array constitué de \(1\) et de longueur identique à celle de la variable
endog. Les poids des variances sont utilisés lorsqueendogreprésente une moyenne. Cela repose sur l’hypothèse que l’inverse de la variance est proportionnel au poids - une observation jugée plus crédible devrait avoir moins de variance et donc avoir plus de poids.missing:strLes options disponibles sont
none,drop, etraise. Sinone, aucune vérification des valeursnann’est effectuée.dropfait que toutes les observations avec desnansont abandonnées.raisesignale une erreur. La valeur par défaut estnone.
On commence par charger les paquets nécessaires, entre autres matplotlib.pyplot pour le traçage, numpy pour la manipulation des matrices et vecteurs et la génération aléatoire, ainsi que pandas pour le stockage des données.
# Affichage avec la bibliothèque graphique intégrée à Notebook
%matplotlib inline
import numpy as np
import statsmodels.api as sm
from scipy import stats
from matplotlib import pyplot as plt
plt.rc("figure", figsize=(16,8))
plt.rc("font", size=14)
GLM avec Réponse Binomiale#
Dans un premier temps, on commence par ajuster un modèle linéaire généralisé à une variable expliquée binomiale (binaire).
Pour ce faire, on invoque le jeu de données Star98, concernent les résultats du programme STAR mis en place par l’instance pédagogique de California lors de 1998. Les données mesurent les tests standardisés du département californien de l’éducation qui a exigé l’évaluation des élèves de la 2ème à la 11ème année par le test Stanford 9 sur une variété de sujets. Ce jeu de données compore 303 enregistrements. La variable de réponse représente le nombre d’élèves de 9ème année ayant obtenu un score supérieur à la valeur médiane nationale à l’examen de mathématiques.
print(sm.datasets.star98.NOTE)
::
Number of Observations - 303 (counties in California).
Number of Variables - 13 and 8 interaction terms.
Definition of variables names::
NABOVE - Total number of students above the national median for the
math section.
NBELOW - Total number of students below the national median for the
math section.
LOWINC - Percentage of low income students
PERASIAN - Percentage of Asian student
PERBLACK - Percentage of black students
PERHISP - Percentage of Hispanic students
PERMINTE - Percentage of minority teachers
AVYRSEXP - Sum of teachers' years in educational service divided by the
number of teachers.
AVSALK - Total salary budget including benefits divided by the number
of full-time teachers (in thousands)
PERSPENK - Per-pupil spending (in thousands)
PTRATIO - Pupil-teacher ratio.
PCTAF - Percentage of students taking UC/CSU prep courses
PCTCHRT - Percentage of charter schools
PCTYRRND - Percentage of year-round schools
The below variables are interaction terms of the variables defined
above.
PERMINTE_AVYRSEXP
PEMINTE_AVSAL
AVYRSEXP_AVSAL
PERSPEN_PTRATIO
PERSPEN_PCTAF
PTRATIO_PCTAF
PERMINTE_AVTRSEXP_AVSAL
PERSPEN_PTRATIO_PCTAF
On importe d’emblée le jeu de données, et on ajoute un terme constant aux variables expliquées exogènes :
data = sm.datasets.star98.load()
data.exog = sm.add_constant(data.exog, prepend=False)
La variable de réponse correspond au couple \(\rm{[Succès :}\) NABOVE \(\rm{,Échec :}\) NBELOW \(]\).
print(data.endog.head())
NABOVE NBELOW
0 452.0 355.0
1 144.0 40.0
2 337.0 234.0
3 395.0 178.0
4 8.0 57.0
Les variables indépendantes comportent toutes les autres variables décrites ci-dessus, ainsi que les termes d’interaction :
print(data.exog.head())
LOWINC PERASIAN PERBLACK PERHISP PERMINTE AVYRSEXP AVSALK \
0 34.39730 23.299300 14.235280 11.411120 15.91837 14.70646 59.15732
1 17.36507 29.328380 8.234897 9.314884 13.63636 16.08324 59.50397
2 32.64324 9.226386 42.406310 13.543720 28.83436 14.59559 60.56992
3 11.90953 13.883090 3.796973 11.443110 11.11111 14.38939 58.33411
4 36.88889 12.187500 76.875000 7.604167 43.58974 13.90568 63.15364
PERSPENK PTRATIO PCTAF ... PCTYRRND PERMINTE_AVYRSEXP \
0 4.445207 21.71025 57.03276 ... 22.222220 234.102872
1 5.267598 20.44278 64.62264 ... 0.000000 219.316851
2 5.482922 18.95419 53.94191 ... 0.000000 420.854496
3 4.165093 21.63539 49.06103 ... 7.142857 159.882095
4 4.324902 18.77984 52.38095 ... 0.000000 606.144976
PERMINTE_AVSAL AVYRSEXP_AVSAL PERSPEN_PTRATIO PERSPEN_PCTAF \
0 941.68811 869.9948 96.50656 253.52242
1 811.41756 957.0166 107.68435 340.40609
2 1746.49488 884.0537 103.92435 295.75929
3 648.15671 839.3923 90.11341 204.34375
4 2752.85075 878.1943 81.22097 226.54248
PTRATIO_PCTAF PERMINTE_AVYRSEXP_AVSAL PERSPEN_PTRATIO_PCTAF const
0 1238.1955 13848.8985 5504.0352 1.0
1 1321.0664 13050.2233 6958.8468 1.0
2 1022.4252 25491.1232 5605.8777 1.0
3 1061.4545 9326.5797 4421.0568 1.0
4 983.7059 38280.2616 4254.4314 1.0
[5 rows x 21 columns]
À présent, on ajuste un modèle linéaire généralisé, en précisant la loi binomiale comme distribution de la réponse. Après, on affiche le résultat :
glm_binom = sm.GLM(data.endog, data.exog, family=sm.families.Binomial())
res = glm_binom.fit()
print(res.summary())
Generalized Linear Model Regression Results
================================================================================
Dep. Variable: ['NABOVE', 'NBELOW'] No. Observations: 303
Model: GLM Df Residuals: 282
Model Family: Binomial Df Model: 20
Link Function: Logit Scale: 1.0000
Method: IRLS Log-Likelihood: -2998.6
Date: Thu, 05 Jan 2023 Deviance: 4078.8
Time: 23:23:56 Pearson chi2: 4.05e+03
No. Iterations: 5 Pseudo R-squ. (CS): 1.000
Covariance Type: nonrobust
===========================================================================================
coef std err z P>|z| [0.025 0.975]
-------------------------------------------------------------------------------------------
LOWINC -0.0168 0.000 -38.749 0.000 -0.018 -0.016
PERASIAN 0.0099 0.001 16.505 0.000 0.009 0.011
PERBLACK -0.0187 0.001 -25.182 0.000 -0.020 -0.017
PERHISP -0.0142 0.000 -32.818 0.000 -0.015 -0.013
PERMINTE 0.2545 0.030 8.498 0.000 0.196 0.313
AVYRSEXP 0.2407 0.057 4.212 0.000 0.129 0.353
AVSALK 0.0804 0.014 5.775 0.000 0.053 0.108
PERSPENK -1.9522 0.317 -6.162 0.000 -2.573 -1.331
PTRATIO -0.3341 0.061 -5.453 0.000 -0.454 -0.214
PCTAF -0.1690 0.033 -5.169 0.000 -0.233 -0.105
PCTCHRT 0.0049 0.001 3.921 0.000 0.002 0.007
PCTYRRND -0.0036 0.000 -15.878 0.000 -0.004 -0.003
PERMINTE_AVYRSEXP -0.0141 0.002 -7.391 0.000 -0.018 -0.010
PERMINTE_AVSAL -0.0040 0.000 -8.450 0.000 -0.005 -0.003
AVYRSEXP_AVSAL -0.0039 0.001 -4.059 0.000 -0.006 -0.002
PERSPEN_PTRATIO 0.0917 0.015 6.321 0.000 0.063 0.120
PERSPEN_PCTAF 0.0490 0.007 6.574 0.000 0.034 0.064
PTRATIO_PCTAF 0.0080 0.001 5.362 0.000 0.005 0.011
PERMINTE_AVYRSEXP_AVSAL 0.0002 2.99e-05 7.428 0.000 0.000 0.000
PERSPEN_PTRATIO_PCTAF -0.0022 0.000 -6.445 0.000 -0.003 -0.002
const 2.9589 1.547 1.913 0.056 -0.073 5.990
===========================================================================================
Le nombre d’épreuves binomiales (en incorporant les fréquences pour chaque observations) est :
print("Nombre total d'épreuves :", data.endog.iloc[:, 0].sum())
Nombre total d'épreuves : 108418.0
Les valeurs de la statistique de Student pour les test élémentaires d’influence de chaque variable explicatives peuvent être récupérés au travers de :
print(res.tvalues)
LOWINC -38.749083
PERASIAN 16.504736
PERBLACK -25.182189
PERHISP -32.817913
PERMINTE 8.498271
AVYRSEXP 4.212479
AVSALK 5.774998
PERSPENK -6.161911
PTRATIO -5.453217
PCTAF -5.168654
PCTCHRT 3.921200
PCTYRRND -15.878260
PERMINTE_AVYRSEXP -7.390931
PERMINTE_AVSAL -8.449639
AVYRSEXP_AVSAL -4.059162
PERSPEN_PTRATIO 6.321099
PERSPEN_PCTAF 6.574347
PTRATIO_PCTAF 5.362290
PERMINTE_AVYRSEXP_AVSAL 7.428064
PERSPEN_PTRATIO_PCTAF -6.445137
const 1.913012
dtype: float64
Il s’avère que toutes les réalisations de la statistique du test de Student sont toutes significativement supérieures à \(0\), les variables explicatives ont ainsi toutes un impact sur la variable de réponse.
Pour confirmer ce constat, nous fixons toutes les variables explicatives à une constante égale à leur moyenne et on varie la variable LOWINC (en première colonne) dénotant le pourcentage des étudiants à faibles revenus pour évaluer son influence sur le succès dans l’examen national de mathématiques.
La méthode scoreatpercentile() de stats permet de calculer le nombre d’unités inférieurs à un quantile d’ordre passé en paramètre.
m = data.exog.mean(axis=0)
m25 = m.copy()
m25.iloc[0] = stats.scoreatpercentile(data.exog.iloc[:,0], 25)
m75 = m.copy()
m75.iloc[0] = stats.scoreatpercentile(data.exog.iloc[:,0], 75)
L’intervalle interquartile pour le pourcentage des étudiants à faibles revenus est donc :
resp_25 = res.predict(m25)
resp_75 = res.predict(m75)
diff = resp_75 - resp_25
print("%2.4f%%" % (diff*100))
-11.8753%
Ensuite, on représente les résultats ainsi générés dans des tracés.
# Nombre d'observations
n = res.nobs
# Valeurs observées de la variable expliquée NABOVE+NBELOW/2
y = data.endog.iloc[:,0]/data.endog.sum(1)
# Valeurs ajustées
yhat = res.mu
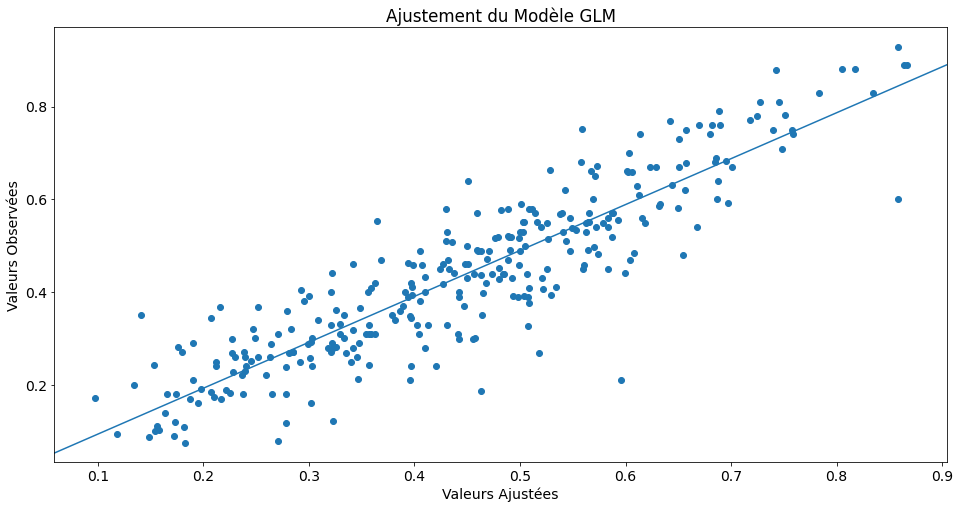
La fonction abline_plot permet de tracer des droites d’ajustement ou de régression à un nuage de points.
from statsmodels.graphics.api import abline_plot
fig, ax = plt.subplots()
ax.scatter(yhat, y)
line_fit = sm.OLS(y, sm.add_constant(yhat, prepend=True)).fit()
abline_plot(model_results=line_fit, ax=ax)
ax.set_title('Ajustement du Modèle GLM')
ax.set_ylabel('Valeurs Observées')
ax.set_xlabel('Valeurs Ajustées')
Text(0.5, 0, 'Valeurs Ajustées')
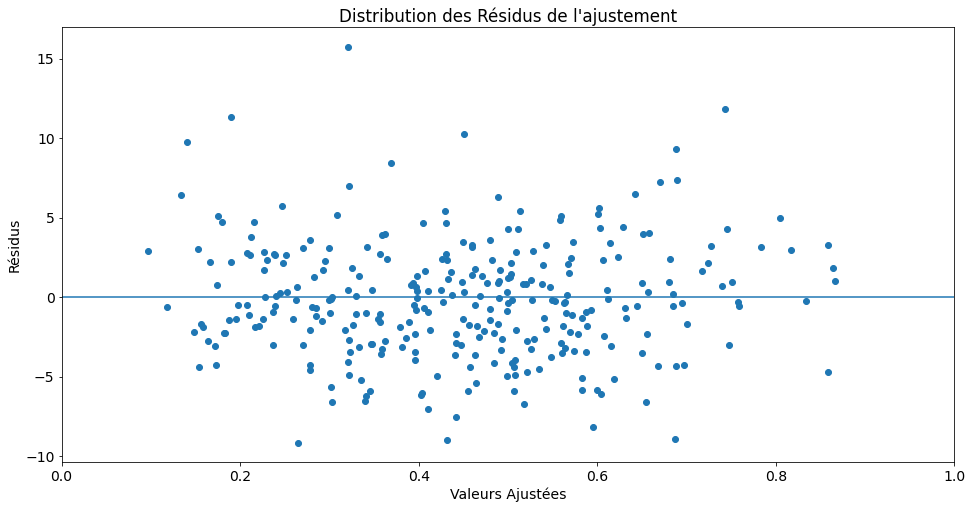
fig, ax = plt.subplots()
ax.scatter(yhat, res.resid_pearson)
ax.hlines(0, 0, 1)
ax.set_xlim(0, 1)
ax.set_title("Distribution des Résidus de l'ajustement")
ax.set_ylabel('Résidus')
ax.set_xlabel('Valeurs Ajustées')
Text(0.5, 0, 'Valeurs Ajustées')
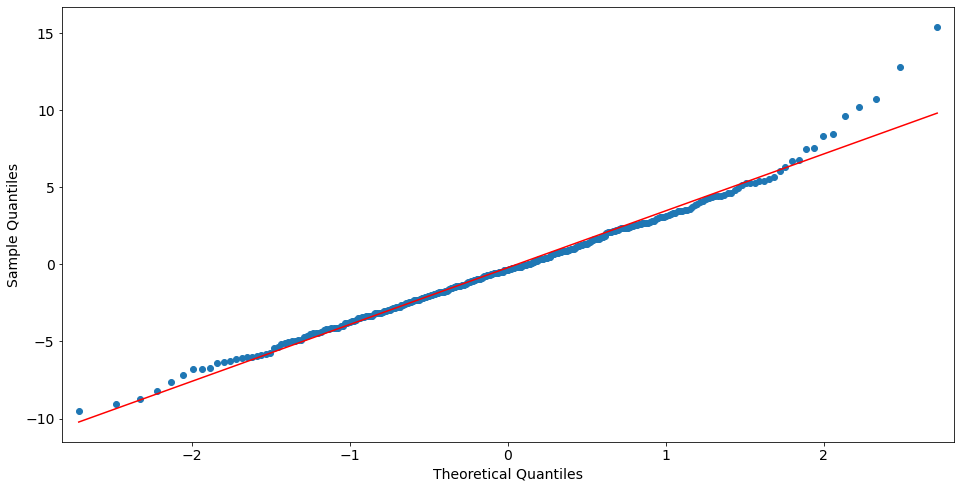
from statsmodels import graphics
graphics.gofplots.qqplot(res.resid_deviance.copy(), line='r')
plt.show()
GLM avec Réponse Gaussienne#
On génére \(100\) observations d’un modèle linéaire généralisé \(\ln(y_i)=\exp(-0.03x_i+0.0001x_i^2-1)+\varepsilon_i\), et on essaie d’adapter un modèle linéaire généralisé dessus, en précisant une distribution gaussienne à la réponse avec une fonction de lien logarithmique \(\log\).
n = 100
x = np.arange(n)
np.random.seed(54321)
X = np.column_stack((x,x**2))
X = sm.add_constant(X, prepend=False)
lny = np.exp(-(.03*x + .0001*x**2 - 1.0)) + .001 * np.random.rand(n)
gauss = sm.GLM(lny, X, family=sm.families.Gaussian(sm.families.links.log()))
resultats = gauss.fit()
print(resultats.summary())
Generalized Linear Model Regression Results
==============================================================================
Dep. Variable: y No. Observations: 100
Model: GLM Df Residuals: 97
Model Family: Gaussian Df Model: 2
Link Function: log Scale: 1.0531e-07
Method: IRLS Log-Likelihood: 662.92
Date: Thu, 05 Jan 2023 Deviance: 1.0215e-05
Time: 23:23:57 Pearson chi2: 1.02e-05
No. Iterations: 7 Pseudo R-squ. (CS): 1.000
Covariance Type: nonrobust
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
x1 -0.0300 5.6e-06 -5361.316 0.000 -0.030 -0.030
x2 -9.939e-05 1.05e-07 -951.091 0.000 -9.96e-05 -9.92e-05
const 1.0003 5.39e-05 1.86e+04 0.000 1.000 1.000
==============================================================================
Conclusion
Le pseudo-coefficient de détermination de Cox & Snell \(R_{\text{CS}}^{2}=1-\left({\frac {L_{0}}{L_{M}}}\right)^{2/n}\), correspondant à l’équivalent du coefficient de détermination ordinaire pour les GLMs est égal à \(1\), confirmant le modèle théorique ci-dessus.
