Analyse de la Variance (ANOVA)
Analyse de la Variance (ANOVA)#
En statistique, l’analyse de la variance (terme souvent abrégé par le terme anglais ANOVA : Analysis of Variance) est un ensemble de modèles statistiques utilisés pour vérifier si les moyennes des groupes proviennent d’une même population. Les groupes correspondent aux modalités d’une variable qualitative et les moyennes sont calculés à partir d’une variable continue. Ce test s’applique lorsque l’on mesure une ou plusieurs variables explicatives catégorielle (appelées alors facteurs de variabilité, leurs différentes modalités étant parfois appelées « niveaux ») qui ont de l’influence sur la loi d’une variable continue à expliquer.
Autrement dit
L’analyse de la variance permet d’étudier le comportement d’une variable quantitative à expliquer en fonction d’une ou de plusieurs variables qualitatives, aussi appelées nominales catégorielles.
La méthode à utiliser pour réaliser des analyses de la variance du paquet statsmodels est anova_lm, en précisant les modèles statistiques à comparer en paramètres.
Pour examiner l’utilisation de cette méthode, on
%matplotlib inline
from urllib.request import urlopen
import numpy as np
np.set_printoptions(precision=4, suppress=True)
import pandas as pd
pd.set_option("display.width", 100)
import matplotlib.pyplot as plt
from statsmodels.formula.api import ols
from statsmodels.graphics.api import interaction_plot, abline_plot
from statsmodels.stats.anova import anova_lm
Le jeu de données utilisé constitue un ensemble de \(46\) observations des salaires d’un groupe d’employés selon leur expérience, laquelle est une variable numérique variant dans \([0,20]\).
url = "http://stats191.stanford.edu/data/salary.table"
fh = urlopen(url)
salary_table = pd.read_table(fh)
salary_table.to_csv("salary.table")
E = salary_table.E
M = salary_table.M
X = salary_table.X
S = salary_table.S
plt.figure(figsize=(20, 12))
symbols = ["D", "^"]
colors = ["r", "g", "blue"]
factor_groups = salary_table.groupby(["E", "M"])
for values, group in factor_groups:
i, j = values
plt.scatter(group["X"], group["S"], marker=symbols[j], color=colors[i - 1], s=144)
plt.xlabel("Expérience")
plt.ylabel("Salaire")
Text(0, 0.5, 'Salaire')
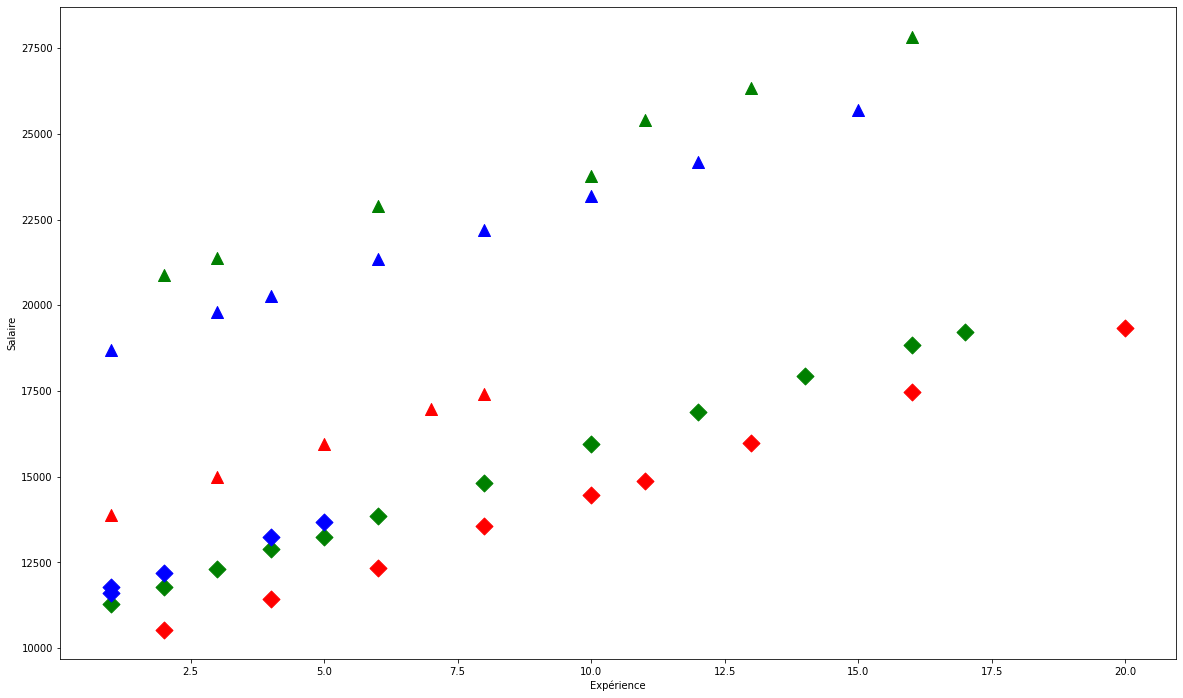
On ajuste un modèle linéaire des moindres carrés ordinaires sur les données en question, moyennant la spécification par les formules (type R).
formula = "S ~ C(E) + C(M) + X"
lm = ols(formula, salary_table).fit()
print(lm.summary())
OLS Regression Results
==============================================================================
Dep. Variable: S R-squared: 0.957
Model: OLS Adj. R-squared: 0.953
Method: Least Squares F-statistic: 226.8
Date: Thu, 05 Jan 2023 Prob (F-statistic): 2.23e-27
Time: 23:24:13 Log-Likelihood: -381.63
No. Observations: 46 AIC: 773.3
Df Residuals: 41 BIC: 782.4
Df Model: 4
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 8035.5976 386.689 20.781 0.000 7254.663 8816.532
C(E)[T.2] 3144.0352 361.968 8.686 0.000 2413.025 3875.045
C(E)[T.3] 2996.2103 411.753 7.277 0.000 2164.659 3827.762
C(M)[T.1] 6883.5310 313.919 21.928 0.000 6249.559 7517.503
X 546.1840 30.519 17.896 0.000 484.549 607.819
==============================================================================
Omnibus: 2.293 Durbin-Watson: 2.237
Prob(Omnibus): 0.318 Jarque-Bera (JB): 1.362
Skew: -0.077 Prob(JB): 0.506
Kurtosis: 2.171 Cond. No. 33.5
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
On récupère l’influence sur la régression de chaque observation au travers de la méthode get_influence() :
infl = lm.get_influence()
print(infl.summary_table())
==================================================================================================
obs endog fitted Cook's student. hat diag dffits ext.stud. dffits
value d residual internal residual
--------------------------------------------------------------------------------------------------
0 13876.000 15465.313 0.104 -1.683 0.155 -0.722 -1.723 -0.739
1 11608.000 11577.992 0.000 0.031 0.130 0.012 0.031 0.012
2 18701.000 18461.523 0.001 0.247 0.109 0.086 0.244 0.085
3 11283.000 11725.817 0.005 -0.458 0.113 -0.163 -0.453 -0.162
4 11767.000 11577.992 0.001 0.197 0.130 0.076 0.195 0.075
5 20872.000 19155.532 0.092 1.787 0.126 0.678 1.838 0.698
6 11772.000 12272.001 0.006 -0.513 0.101 -0.172 -0.509 -0.170
7 10535.000 9127.966 0.056 1.457 0.116 0.529 1.478 0.537
8 12195.000 12124.176 0.000 0.074 0.123 0.028 0.073 0.027
9 12313.000 12818.185 0.005 -0.516 0.091 -0.163 -0.511 -0.161
10 14975.000 16557.681 0.084 -1.655 0.134 -0.650 -1.692 -0.664
11 21371.000 19701.716 0.078 1.728 0.116 0.624 1.772 0.640
12 19800.000 19553.891 0.001 0.252 0.096 0.082 0.249 0.081
13 11417.000 10220.334 0.033 1.227 0.098 0.405 1.234 0.408
14 20263.000 20100.075 0.001 0.166 0.093 0.053 0.165 0.053
15 13231.000 13216.544 0.000 0.015 0.114 0.005 0.015 0.005
16 12884.000 13364.369 0.004 -0.488 0.082 -0.146 -0.483 -0.145
17 13245.000 13910.553 0.007 -0.674 0.075 -0.192 -0.669 -0.191
18 13677.000 13762.728 0.000 -0.089 0.113 -0.032 -0.087 -0.031
19 15965.000 17650.049 0.082 -1.747 0.119 -0.642 -1.794 -0.659
20 12336.000 11312.702 0.021 1.043 0.087 0.323 1.044 0.323
21 21352.000 21192.443 0.001 0.163 0.091 0.052 0.161 0.051
22 13839.000 14456.737 0.006 -0.624 0.070 -0.171 -0.619 -0.170
23 22884.000 21340.268 0.052 1.579 0.095 0.511 1.610 0.521
24 16978.000 18742.417 0.083 -1.822 0.111 -0.644 -1.877 -0.664
25 14803.000 15549.105 0.008 -0.751 0.065 -0.199 -0.747 -0.198
26 17404.000 19288.601 0.093 -1.944 0.110 -0.684 -2.016 -0.709
27 22184.000 22284.811 0.000 -0.103 0.096 -0.034 -0.102 -0.033
28 13548.000 12405.070 0.025 1.162 0.083 0.350 1.167 0.352
29 14467.000 13497.438 0.018 0.987 0.086 0.304 0.987 0.304
30 15942.000 16641.473 0.007 -0.705 0.068 -0.190 -0.701 -0.189
31 23174.000 23377.179 0.001 -0.209 0.108 -0.073 -0.207 -0.072
32 23780.000 23525.004 0.001 0.260 0.092 0.083 0.257 0.082
33 25410.000 24071.188 0.040 1.370 0.096 0.446 1.386 0.451
34 14861.000 14043.622 0.014 0.834 0.091 0.263 0.831 0.262
35 16882.000 17733.841 0.012 -0.863 0.077 -0.249 -0.860 -0.249
36 24170.000 24469.547 0.003 -0.312 0.127 -0.119 -0.309 -0.118
37 15990.000 15135.990 0.018 0.878 0.104 0.300 0.876 0.299
38 26330.000 25163.556 0.035 1.202 0.109 0.420 1.209 0.422
39 17949.000 18826.209 0.017 -0.897 0.093 -0.288 -0.895 -0.287
40 25685.000 26108.099 0.008 -0.452 0.169 -0.204 -0.447 -0.202
41 27837.000 26802.108 0.039 1.087 0.141 0.440 1.089 0.441
42 18838.000 19918.577 0.033 -1.119 0.117 -0.407 -1.123 -0.408
43 17483.000 16774.542 0.018 0.743 0.138 0.297 0.739 0.295
44 19207.000 20464.761 0.052 -1.313 0.131 -0.511 -1.325 -0.515
45 19346.000 18959.278 0.009 0.423 0.208 0.216 0.419 0.214
==================================================================================================
À présent, on trace le graphique des résidus pour chaque groupe séparément :
resid = lm.resid
plt.figure(figsize=(20, 12))
for values, group in factor_groups:
i, j = values
group_num = i * 2 + j - 1
x = [group_num] * len(group)
plt.scatter(x,resid[group.index],marker=symbols[j],color=colors[i - 1],s=144,edgecolors="black")
plt.xlabel("Groupes")
plt.ylabel("Résidus")
Text(0, 0.5, 'Résidus')
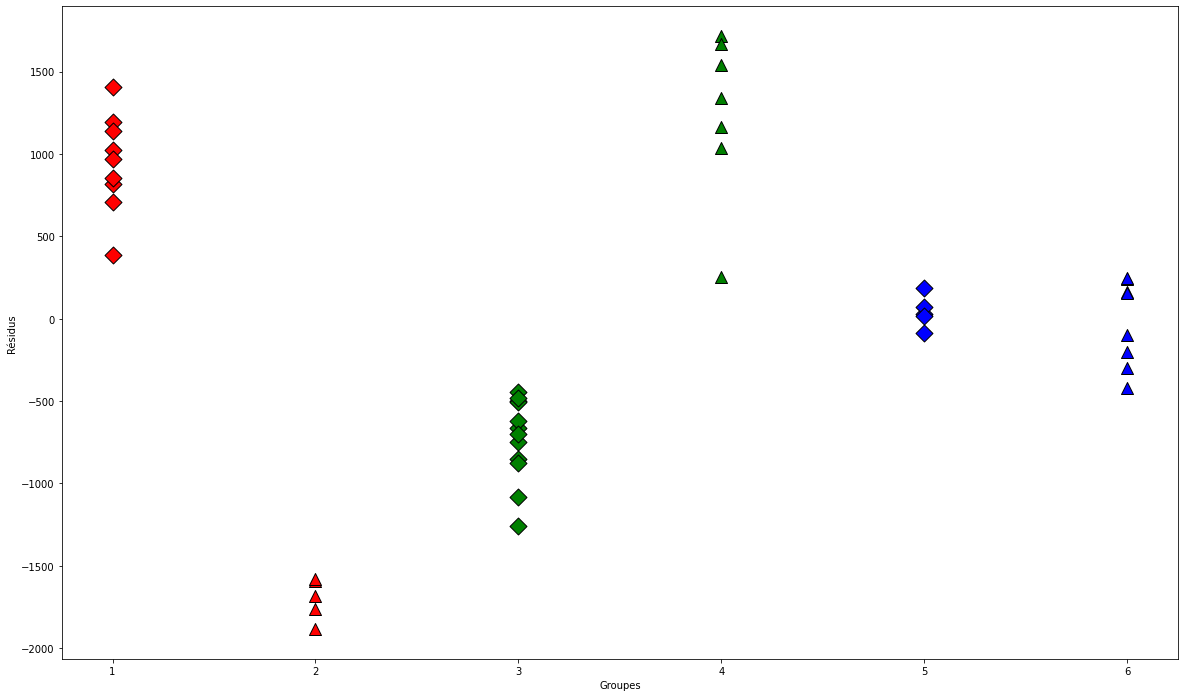
Ensuite, on ajuste un modèle pour le comparer au premier via l’analyse de la variance.
interX_lm = ols("S ~ C(E) * X + C(M)", salary_table).fit()
print(interX_lm.summary())
OLS Regression Results
==============================================================================
Dep. Variable: S R-squared: 0.961
Model: OLS Adj. R-squared: 0.955
Method: Least Squares F-statistic: 158.6
Date: Thu, 05 Jan 2023 Prob (F-statistic): 8.23e-26
Time: 23:24:14 Log-Likelihood: -379.47
No. Observations: 46 AIC: 772.9
Df Residuals: 39 BIC: 785.7
Df Model: 6
Covariance Type: nonrobust
===============================================================================
coef std err t P>|t| [0.025 0.975]
-------------------------------------------------------------------------------
Intercept 7256.2800 549.494 13.205 0.000 6144.824 8367.736
C(E)[T.2] 4172.5045 674.966 6.182 0.000 2807.256 5537.753
C(E)[T.3] 3946.3649 686.693 5.747 0.000 2557.396 5335.333
C(M)[T.1] 7102.4539 333.442 21.300 0.000 6428.005 7776.903
X 632.2878 53.185 11.888 0.000 524.710 739.865
C(E)[T.2]:X -125.5147 69.863 -1.797 0.080 -266.826 15.796
C(E)[T.3]:X -141.2741 89.281 -1.582 0.122 -321.861 39.313
==============================================================================
Omnibus: 0.432 Durbin-Watson: 2.179
Prob(Omnibus): 0.806 Jarque-Bera (JB): 0.590
Skew: 0.144 Prob(JB): 0.744
Kurtosis: 2.526 Cond. No. 69.7
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
À présent, on compare les deux modèles élaborés avec la fonction anova_lm
from statsmodels.stats.api import anova_lm
table1 = anova_lm(lm, interX_lm)
print(table1)
interM_lm = ols("S ~ X + C(E)*C(M)", data=salary_table).fit()
table2 = anova_lm(lm, interM_lm)
print(table2)
df_resid ssr df_diff ss_diff F Pr(>F)
0 41.0 4.328072e+07 0.0 NaN NaN NaN
1 39.0 3.941068e+07 2.0 3.870040e+06 1.914856 0.160964
df_resid ssr df_diff ss_diff F Pr(>F)
0 41.0 4.328072e+07 0.0 NaN NaN NaN
1 39.0 1.178168e+06 2.0 4.210255e+07 696.844466 3.025504e-31
Conclusion
Dès lors que la première valeur du seuil critique (\(p\)-value) est supérieure à \(5\%\), alors le deuxième modèle interX_lm est significativement meilleur. Le troisième modèle interM_lm ne contribue pas significativement mieux par rapport au modèle de base, dès lors que sa \(p\)-valeur est inférieure à \(5\%\).
